円周率の小数点以下に現れる数値

(2018/03/22 8:07:53 created.)

ふと円周率に思いをはせることがあり（かなり頭おかＣ）、
小数点以下に現れる 0 から 9 の数の出現率は
どのような分布になっているのだろう、と気になってしまった。

気になってしまったものはしょうがない。
というわけで C# コードで簡単に調べてみたよ。

Program.cs

```
namespace PiTest
```
```
{
```
```
    using System;
```
```
    using System.Linq;
```
```
    using System.Text;
```
```
 
```
```
    internal class Program
```
```
    {
```

        static void Main(string[] args)

```
        {
```

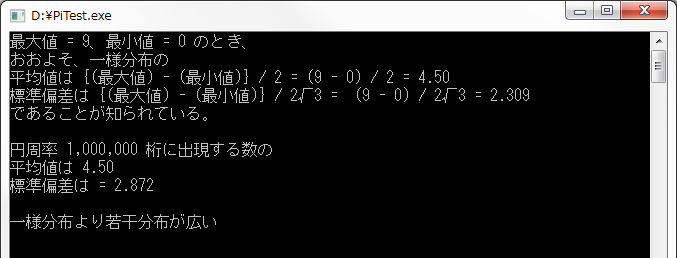
            Console.WriteLine("最大値 = 9、最小値 = 0 のとき、");

            Console.WriteLine("おおよそ、一様分布の");

            Console.WriteLine("平均値は {(最大値) - (最小値)} / 2 = (9 - 0) / 2 = 4.50");

            Console.WriteLine("標準偏差は {(最大値) - (最小値)} / 2√3 =  (9 - 0) / 2√3 = " + (9 / 2 / Math.Sqrt(3.0)).ToString("#0.000"));

            Console.WriteLine("であることが知られている。");

            Console.WriteLine();

```
 
```

            var nums = ASCIIEncoding.ASCII.GetBytes(Constants.PiString).Select(x => x - 0x30).ToArray();

            Console.WriteLine("円周率 " + nums.Length.ToString("N0") +" 桁に出現する数の");

```
 
```

            var ave = nums.Average();

            var stdev = Math.Sqrt(((double)nums.Select(x => x * x).Sum() / nums.Length - ave * ave));

            Console.WriteLine("平均値は " + ave.ToString("#0.00"));

            Console.WriteLine("標準偏差は = " + stdev.ToString("#0.000"));

            Console.WriteLine();

```
 
```

            Console.WriteLine("一様分布より若干分布が広い");

```
 
```

            Console.ReadKey();

```
        }
```
```
    }
```
```
}
```

Constants.PiString は static な string 型で、
円周率の小数点以下の数値を文字列として 1,000,000 桁分保持しています。
というのも、web 上で円周率を調べたらこの桁であれば
テキストデータで掲載されていたので、
それをそのまま流用させていただいたというだけです。

実行結果がこちら。

標準偏差が一様分布のものよりもやや大きめ、という結果でした。
円周率は調べ出すと人生終わるらしいので程々にしておきます。

<< 古い記事へ
シーケンスを n 個毎に分割する

新しい記事へ >>
Keras による学習モデルを変...